ANALYSE PHARMACOCINÉTIQUE

L’intérêt en pratique clinique de la pharmacocinétique descriptive telle que nous venons de l’évoquer est d’expliquer la cinétique d’action des produits avec ses variations, et de définir les meilleurs schémas posologiques possible en fonction des associations médicamenteuses, du terrain et de la nature de l’intervention projetée. Pour cela, il nous faut convertir des notions générales en concentrations, puis en doses. Pour nous aider nous ne disposons pratiquement chez l’homme que de prélèvements sanguins et urinaires, de la mesure de quelques effets pharmacodynamiques (électroencéphalogramme [EEG], monitorage de la curarisation) et de techniques analytiques de dosage des médicaments.

Amélioration des techniques de dosage des médicaments, facteur de meilleure analyse pharmacocinétique

L’analyse pharmacocinétique quantitative est entièrement dépendante de la mesure des concentrations de médicaments. Cette mesure n’est pas toujours aisée, et les progrès de la pharmacocinétique ont été liés à l’amélioration des techniques de séparation et de dosage des agents dans les liquides biologiques (chromatographie, méthodes immunoenzymatiques, utilisation d’isotopes radioactifs…). Ainsi par exemple la décomposition d’une courbe de décroissance plasmatique peut s’arrêter à deux exponentielles si la technique de dosage, peu sensible, ne permet pas de détecter les concentrations résiduelles correspondant à une troisième exponentielle. L’amélioration de la sensibilité des dosages de certains agents a permis une meilleure analyse de leur élimination : les premières publications décrivaient un modèle à deux compartiments puis un troisième compartiment est apparu au fil du temps. Seules des techniques très sensibles radio-immunologiques permettent de mesurer les concentrations de certains agents très puissants (sufentanil). L’amélioration des techniques de séparation a parfois permis de discriminer le composé natif de ses métabolites (morphine).

La mesure extemporanée des concentrations d’halogénés dans les mélanges gazeux a transformé l’administration de ces agents et a considérablement amélioré la sécurité des patients lors de leur usage.

Les techniques de chimie sèche permettront dans un avenir proche d’avoir une estimation très rapide de la concentration plasmatique de certains agents à index thérapeutique étroit (lidocaïne par exemple) pour guider leur administration soit en perfusion massique, soit mieux en perfusion à objectif de concentration (cf infra) avec adaptation bayesienne dans les situations où la pharmacocinétique peut être altérée (par exemple : défaillance circulatoire).

Analyse compartimentale. Modèles pharmacocinétiques

Décomposition de la courbe de décroissance des concentrations plasmatiques après une dose unique

L’administration intraveineuse d’une dose unique de médicament génère dans le sang une concentration dont la valeur décroît au cours du temps. La courbe de décroissance des concentrations plasmatiques après une dose unique peut toujours être décomposée en une somme de n exponentielles de forme : où C (t) représente la concentration au temps t et D la dose administrée. Cette équation est la première représentation du ” modèle ” pharmacocinétique.

La construction des modèles pharmacocinétiques représente un compromis entre une description précise des données et un traitement mathématique réalisable. Souvent l’adjonction d’autres exponentielles au modèle (l’augmentation de n) permet de mieux décrire les données. Cependant, le fait d’ajouter des exponentielles diminue généralement la fiabilité de l’estimation de chaque coefficient et de chaque exposant et augmente considérablement le fardeau mathématique que représentent ces modèles. C’est pourquoi la plupart d’entre eux se limitent à deux ou trois exponentielles.

Le modèle pharmacocinétique représenté ci-dessus a quelques caractéristiques utiles, qui expliquent sa popularité persistante en analyse pharmacocinétique.

Dans la zone thérapeutique, l’immense majorité des agents, et en tous cas tous ceux qui sont utilisés en anesthésie, répondent au principe de linéarité : si vous doublez la dose, vous doublez la concentration. Considérons l’équation ci-dessus pour deux valeurs de D (l’apport de produit), l’une étant exactement le double de l’autre. L’équation prédit que la C (t) sera deux fois plus élevée si l’apport est deux fois plus important : le modèle suit lui aussi le principe de linéarité. Plus généralement, la linéarité implique que le système se comporte en suivant le théorème de superposition. Ce théorème stipule que la réponse d’un système linéaire ayant des apports multiples peut être calculée en déterminant la réponse de chaque apport individuel et en faisant la somme des réponses élémentaires pour obtenir la réponse totale. En d’autres termes, lorsqu’un organisme traite chaque dose élémentaire d’agent selon une décroissance polyexponentielle dans le temps, le devenir de chaque dose élémentaire n’influence pas le devenir des autres.

Une autre raison pour laquelle ces modèles restent si populaires est qu’ils peuvent être transformés mathématiquement de la forme polyexponentielle considérée comme peu parlante exposée plus haut en une forme compartimentale plus intuitivement appréhensible, dont la figure 3 propose deux schématisations. L’organisme est considéré vis-à-vis du médicament concerné comme un ensemble de compartiments dans chacun desquels le médicament se trouve à chaque instant à une concentration uniforme(fig 3A). Le produit circule du compartiment central vers les compartiments périphériques et en revient par diffusion passive le long d’un gradient de concentration, à une vitesse dépendante d’une constante de transfert appelée par convention k 1 n pour les transferts du compartiment central (1) vers le compartiment périphérique (n) et kn 1 pour le retour du compartiment n vers le compartiment central. Par postulat, l’élimination définitive se fait à partir du compartiment central selon une constante de transfert appelée k10 (1 = compartiment central, 0 = extérieur). La concentration dans chaque compartiment décroît de façon monoexponentielle en fonction du temps, et il est possible de construire à partir de l’équation polyexponentielle une représentation du devenir de l’agent dans l’organisme, appelée modèle à n compartiments. Ces compartiments peuvent également être représentés par un système de baquets et de tuyaux appelé modèle hydraulique (fig 3B) où les transferts entre compartiments sont représentés par les clairances systémique (Cl1) et intercompartimentales (Cl2, Cl3). Il existe une relation mathématique que nous ne détaillerons pas entre les constantes de l’équation et les microconstantes (constantes de transfert entre les compartiments) des modèles compartimentaux, de même qu’il existe une relation mathématique entre les microconstantes et les macroconstantes que sont les clairances (systémique et intercompartimentales rapide et lente) ou les volumes de distribution (central et périphériques d’équilibration rapide et lente), paramètres fondamentaux du modèle compartimental.

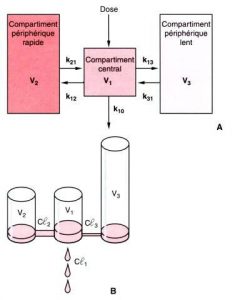
À ces compartiments théoriques ont été associées des réalités physiologiques : le compartiment central (compartiment 1) représente le volume de distribution quasi instantanée et comprend la fraction sanguine de mélange rapide et la captation pulmonaire de premier passage ; les compartiments périphériques sont composés des tissus et des organes dans lesquels la cinétique et l’importance de l’accumulation (ou de la dissipation) de l’agent sont différentes de celles du compartiment central. Dans le modèle tricompartimental, les deux compartiments périphériques peuvent correspondre grossièrement aux tissus splanchniques et aux muscles (équilibration rapide) et au tissu adipeux (équilibration lente). La somme des volumes des compartiments est le volume apparent de distribution à l’équilibre (Vss). C’est la constante de proportionnalité qui lie la concentration plasmatique de l’agent à l’équilibre, à la quantité totale d’agent présente alors dans l’organisme.

Malgré la connotation ” physiologique ” donnée aux modèles compartimentaux, il est important de réaliser que ce ne sont que des transformations mathématiques des fonctions polyexponentielles décrites plus haut et calculées entièrement à partir de concentrations plasmatiques observées. Par conséquent l’interprétation physiologique des volumes et des clairances, à l’exception peut-être de la clairance systémique et du Vss (qui peuvent être calculés indépendamment des modèles, cf infra) est pure spéculation.

Pharmacocinétique de population

En pratique, l’établissement de l’équation initiale pour un agent donné se fait en recherchant la courbe polyexponentielle statistiquement la plus proche de la courbe expérimentale obtenue après administration d’une dose unique. Cette estimation est d’autant plus précise et fiable que le nombre de points (de prélèvements…) est plus grand.

Or ce que l’on recherche en général, ce sont les paramètres pharmacocinétiques moyens qui décrivent une population donnée. Par conséquent, les résultats de plusieurs sujets devront être confrontés pour définir les paramètres pharmacocinétiques moyens, mais la lourdeur de ces protocoles et le nombre de prélèvements nécessaires limitent très rapidement le nombre de sujets concernés. Par ailleurs avec cette approche, les imprécisions statistiques observées chez un ou plusieurs sujets ne sont plus prises en compte pour le calcul des paramètres ” moyens ” qui peuvent donc se trouver entachés d’erreur. Une autre méthode consiste à regrouper tous les prélèvements en provenance des différents sujets (et on peut alors faire moins de prélèvements par sujet en étudiant plus de sujets…), après les avoir harmonisés en fonction de la dose reçue, et à faire une analyse statistique par régression globale sur l’ensemble des points. Cette technique, étonnamment robuste dès lors qu’il s’agit de définir des paramètres moyens, est appelée pharmacocinétique de population [59]. Elle permet en outre de définir les facteurs de variation significatifs pour un agent donné (poids, âge…) et de calculer les coefficients de pondération correspondants.

Modèles physiologiques

Les modèles compartimentaux ont l’avantage de la simplicité mais, comme nous l’avons vu, ce sont des manipulations mathématiques qui ne présentent qu’un aspect très schématique de l’organisme. À l’inverse, un modèle physiologique consiste en un ensemble structurel dont la charpente mathématique tente de représenter au plus près la réalité physiologique des différents organes ou tissus [18]. La complexité d’un modèle physiologique n’est limitée que par deux facteurs : l’existence de données fiables pour les très nombreux paramètres mis en jeu, et la puissance de calcul de l’ordinateur disponible.

La construction d’un modèle physiologique comporte schématiquement trois étapes : on construit d’abord un modèle physiologique chez l’animal, en mesurant les débits régionaux, les clairances métaboliques, les liaisons protéiques etc. On recueille le plus grand nombre possible de données physiologiques chez l’homme (débits, poids d’organes…). En associant au modèle animal des données biochimiques extrapolées à l’homme et les données physiologiques humaines, un modèle physiologique chez l’homme est élaboré que l’on perfectionnera au fur et à mesure de l’acquisition de nouvelles données. Ces systèmes complexes, inapplicables au quotidien, permettent cependant de mieux comprendre par exemple le devenir d’agents qui interfèrent avec leur propre élimination soit par les effets hémodynamiques qu’ils induisent, soit par leur action propre sur les systèmes enzymatiques qui les détruisent (propranolol, halothane…). Comme ils intègrent facilement des données d’évolution dans le temps des paramètres, ils permettent également de simuler des situations importantes en anesthésie-réanimation comme par exemple l’hémorragie aiguë ou la défaillance viscérale.

Application de l’analyse compartimentale à l’anesthésie

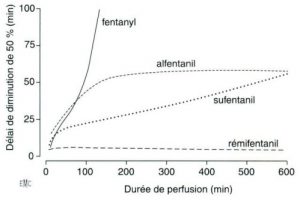
La pharmacocinétique traditionnelle, bien adaptée aux traitements chroniques, nous est d’un maigre secours pour visualiser les mouvements très rapides des agents pendant le cours d’une anesthésie. Il a donc fallu repenser la pharmacocinétique clinique pour l’adapter à la situation très particulière de l’anesthésie. Ainsi est apparu un nouveau paramètre : la demi-vie apparente ou contextuelle (en anglais : context sensitive half fortement dépendante des paramètres de distribution de l’agent, augmente progressivement, de façon plus ou moins importante selon l’agent, avec la durée de la perfusion [31]. Son étude dans des programmes de simulation a permis d’expliquer les différences de comportement d’agents dont la cinétique traditionnelle n’est pas très différente (fentanyl/sufentanil[fig 4]).

Les modèles pharmacocinétiques tricompartimentaux à partir desquels est calculée la demi-vie contextuelle peuvent également nous servir : à simuler un certain nombre de situations cliniques et par là même à réduire les besoins en investigations chez l’homme ; à reconstituer l’évolution de la concentration d’un agent dans certains cas difficiles (par exemple lors d’une expertise médicolégale) ou à partir des schémas posologiques proposés dans la littérature ; à créer de nouveaux schémas posologiques manuels à partir de profils de concentration souhaités ; à construire des abaques avec des courbes d’isoconcentration pour guider les perfusions manuelles ; à piloter des seringues autopousseuses en leur imposant un objectif de concentration plutôt qu’un débit massique (cf infra).

Analyse non compartimentale

Les postulats et les limitations de l’analyse compartimentale ont conduit à rechercher des modes d’analyse plus globaux, mais aboutissant éventuellement à des résultats moins entachés d’erreur. À l’aide de la théorie statistique des moments, et de l’analyse de l’aire sous la courbe des concentrations plasmatiques (AUC : area under the curve), quelques paramètres particulièrement importants peuvent être calculés : la clairance d’élimination (Cl=dose/AUC) ; le temps de résidence moyen (MRT) d’une molécule de l’agent dans l’organisme et le volume de distribution à l’équilibre de l’agent Vss (Vss=Cl × MRT). Les paramètres ainsi calculés ne présument pas de la structure du modèle associé et ils peuvent être considérés comme vrais en toutes circonstances. On doit cependant remarquer que l’analyse des courbes ” de zéro à l’infini ” implique une extrapolation qui sera d’autant moins importante que les prélèvements sanguins auront été poursuivis plus avant dans le temps.

Compartiment au site d’action

Lorsqu’on administre un agent dans le sang, l’effet pharmacologique obtenu n’est pas instantané (par exemple, la perte de connaissance après une administration rapide de thiopental est de plusieurs dizaines de secondes), et l’effet maximal est retardé par rapport au pic de concentration plasmatique. Si l’on postule que l’effet obtenu est proportionnel à la concentration en face des récepteurs, il est tentant d’assimiler la biophase (ensemble des récepteurs de l’agent et de leur environnement immédiat) à un tout petit compartiment dont le volume, négligeable, n’interférerait pas avec le modèle calculé.

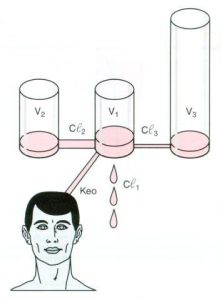
L’évolution de la concentration dans ce compartiment pourrait alors être déduite de l’évolution de la concentration plasmatique, à condition de postuler qu’il n’existe pas de décalage dans le temps (hystérésis) entre l’évolution de la concentration dans la biophase et l’effet pharmacologique obtenu (fig 5). Ce postulat est important car, comme on ne peut pas calculer la concentration dans la biophase, il va falloir la définir par rapport à l’effet qu’elle entraîne. Si, pour un agent donné, nous connaissons les paramètres traditionnels du modèle (par exemple tricompartimental), ainsi que l’ensemble des valeurs possibles de la clairance intercompartimentale vers le compartiment au site d’action, nous pouvons calculer les équations d’un ensemble de courbes représentant l’évolution de la concentration de l’agent dans la biophase et confronter ces courbes à la courbe qui représente l’évolution mesurée de l’effet pharmacologique. La bonne valeur de la clairance intercompartimentale sera celle pour laquelle, par définition, il n’y a pas d’hystérésis entre la courbe de concentration de l’agent et la courbe d’évolution de l’effet.

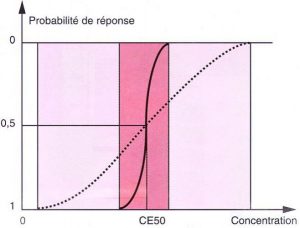
La courbe qui décrit la concentration dans la biophase en fonction de l’intensité de l’effet est dans la grande majorité des cas une sigmoïde (équation de Hill). Selon l’équation de Hill, on peut calculer pour chaque agent, par régression, une concentration correspondent à 50 % de l’effet (CE50). Comme les conditions de liaison protéique dans la biophase sont inconnues, cette CE50 représente en fait la concentration plasmatique qui, à l’équilibre (quand tous les transferts sont annulés), correspondrait au même effet. Cependant, le postulat selon lequel la courbe concentration / effet suit l’équation de Hill n’est pas toujours vrai. Ceci a conduit à l’élaboration de modes de calcul non compartimentaux de la CE50 et de la constante de transfert ke0 [58]. Ces calculs valent ce que vaut la mesure de l’effet. Pour les curares par exemple, nous disposons d’une mesure fiable et reproductible de l’effet. La ke0 des curares est donc une valeur solide. Pour les hypnotiques, le ” bon ” paramètre de mesure de la profondeur de l’anesthésie reste à valider. Lorsqu’on utilise les calculs actuels, fondés sur l’analyse spectrale de l’EEG, il faut garder en mémoire les limitations de cette analyse comme mesure effective de l’effet hypnotique.

Relations pharmacocinétiques / pharmacodynamiques : de la nécessité d’une recherche pharmacodynamique

La plupart des tentatives faites pour comprendre la cinétique d’action d’un agent anesthésique ont été fondées sur une analyse pharmacocinétique. Néanmoins bien souvent une analyse pharmacodynamique est indispensable : si un paramètre évolue de façon continue (par exemple la dépression du twitch lors de la curarisation) et si l’on définit avec précision quelle est la valeur qui correspond à une récupération, la durée d’action de l’agent est simplement le temps nécessaire pour que la concentration au site d’action atteigne la valeur qui correspond à la récupération.

Malheureusement en anesthésie bien des paramètres évoluent de façon binaire et suivent la loi du ” tout ou rien ” : le patient est conscient ou non… Définir la concentration sanguine qui correspond précisément à l’effet pharmacologique recherché (par exemple l’ouverture des yeux) devient aléatoire. On ne peut se fonder sur l’évolution du paramètre chez le patient en cause, mais il faut présager du comportement dudit patient à partir d’études statistiques sur le comportement d’une cohorte de patients. Une courbe doseréponse moyenne est ainsi construite. Elle a en général l’allure d’une sigmoïde dont le point d’inflexion correspond à la CE50 de l’agent. Si la courbe dose-réponse de l’agent pour le paramètre considéré est très abrupte, on pourra caractériser avec précision la bande étroite de concentration correspondant statistiquement à l’apparition (ou à la disparition) de l’effet. En revanche, si la courbe est aplatie, il devient très difficile de faire correspondre une valeur de concentration à une probabilité réaliste d’apparition de l’effet (fig 6). Une façon de répondre à cette difficulté est de faire des études pharmacodynamiques de population pour caractériser plus précisément les courbes dose-réponse et leur donner une correspondance en pratique clinique [4]. La courbe trop aplatie est alors décomposée en une famille de courbes plus verticales de CE50 différentes, définies à partir de covariables significatives (âge, traitements associés…). Selon la valeur de ces covariables, le patient appartient à une courbe spécifique et bien verticalisée autour d’une CE50 particulière. Ainsi par exemple la demi-vie apparente ou contextuelle est un paramètre purement pharmacocinétique et en faire un paramètre de prévision du délai de réveil, bien que cela soit tentant, expose à bien des déboires (si la concentration doit diminuer non pas de 50 mais de 80 % pour atteindre la zone des concentrations de réveil…). Si la concentration correspondant à une probabilité de réveil de 50 % (CE50 pour le réveil) peut être estimée avec une précision raisonnable, il devient beaucoup plus intéressant de calculer (qu’un perfuseur calcule pour nous…) le temps de décroissance, c’est-à-dire le temps nécessaire pour atteindre la CE50 à partir de la concentration de fin de perfusion. Il est donc particulièrement important de définir le plus précisément possible les relations concentration / effet des agents et de leurs associations dans les situations cliniques les plus fréquentes (induction, intubation, incision chirurgicale, fermeture cutanée…) pour guider connaissance de cause la séquence d’administration des agents au cours d’une anesthésie.